Low-order modeling

High-fidelity simulations often require many degrees-of-freedom to resolve all the scales of motion. However, the dynamics of many dissipative systems, like turbulent flows, are expected to lie on a finite-dimensional manifold at long-times. Recently, we have shown for turbulent flows that the dimension of this manifold appears to be far lower than the ambient dimension required to simulate these flows (Linot & Graham, 2020; Linot & Graham, 2023). Furthermore, we have developed data-driven methods to parameterize these manifolds, and forecast dynamics in these coordinate system -- which we refer to as data-driven manifold dynamics (DManD).

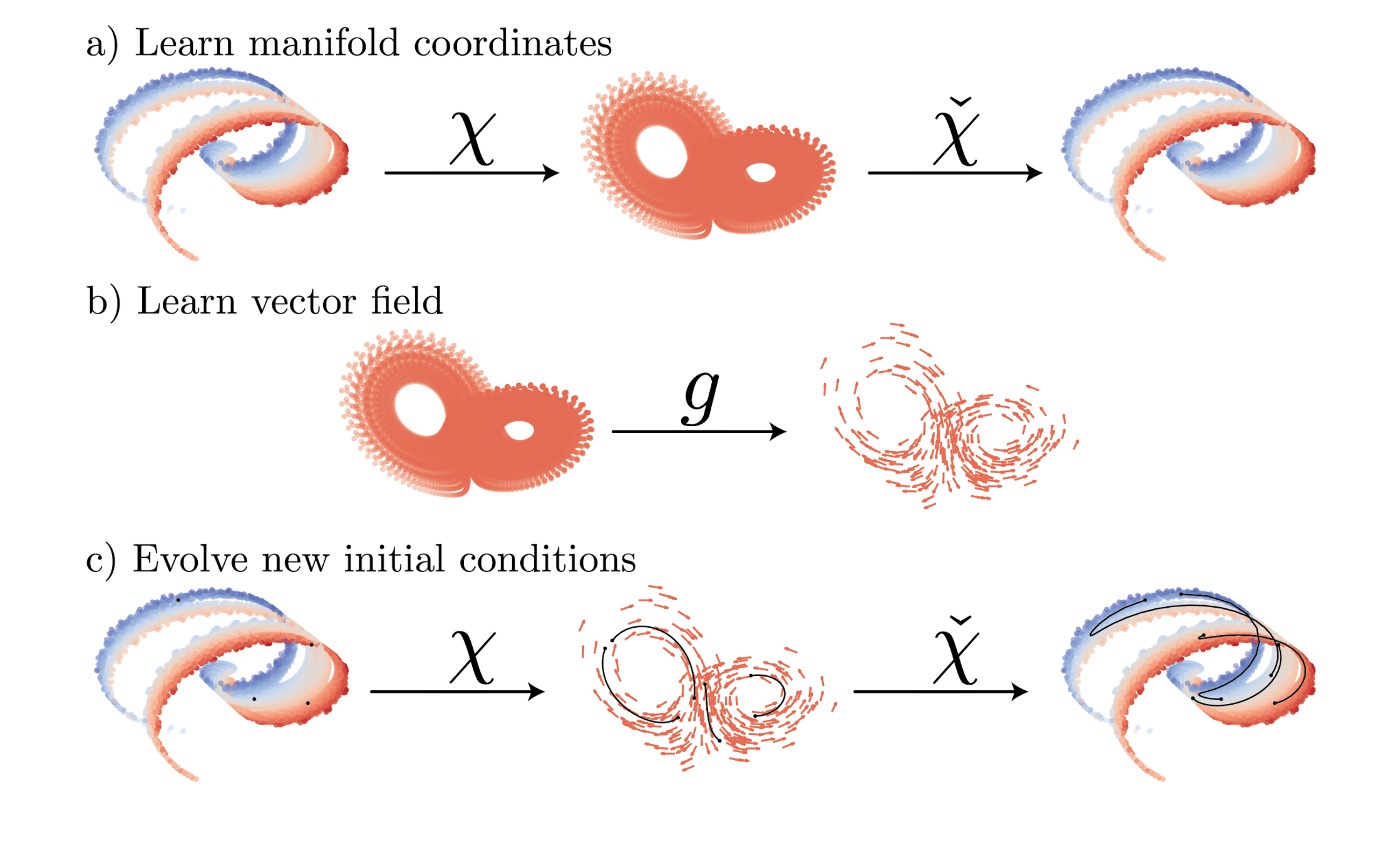
We are primarily concerned with the long-time dynamics (slow dynamics) of these systems. Modeling in a manifold coordinate system offers massive computational benefits, which allows us to rapidly forecast and control these systems. Also, distilling the dynamics down to only the key components could improve our understanding of these systems. Unfortunately, many hurdles still remain before these types of machine learning models can become common place in computational fluid dynamics software. In our group, we are developing methods to reduce or eliminate the data requirements needed to construct low-dimensional models. Some of these approaches include developing techniques to account for system symmetries, spatially distributed flows, and the underlying equations of motion.